一、命题原则
《高等数学》是高等中医药院校药学类、检验类、理工类、人文管理等类专业的一门专业基础课,是理、工、经、管、人文等许多专业的重要课程。
通过教学使学生熟练掌握高等数学的基本理论和基本方法,培养学生具有一定的分析问题和解决问题的能力以及计算能力,运用微积分学知识解决实际问题的能力,为后续课程的学习打下好的基础。因此,考试应有较高信度、效度、必要的区分度和适当的难度。
二、考试形式与成绩评定
期末考试方式为闭卷、笔试,试卷满分为100分,考试时间为120分钟。
三、考查内容和基本要求
第一章 函数
1、考试内容:变量与函数、函数的几种特性、初等函数。
2、考试要求:
(1)掌握函数的概念,函数的几种特性和反函数,复合函数,初等函数的性质。
第二章 极限与连续
1、考试内容:数列的极限;函数的极限;无穷小量与无穷大量;极限运算法则;极限存在准则;两个重要极限;无穷小的比较;函数连续性;闭区间上连续函数的性质。
2、考试要求:
(1)掌握数列极限、函数极限的定义,性质,极限存在准则;能熟练地运用性质、两个重要极限等计算极限。
(2)理解掌握无穷小、无穷大概念,并能用此解相关问题。
(3)掌握函数在点
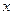 处连续与间断的概念并能解相关问题。
处连续与间断的概念并能解相关问题。
(4)理解闭区间上连续函数的性质并能解决相关问题。
(5)理解初等函数的连续性。
第三章 导数与微分
1、考试内容:导数概念,导数的基本公式与运算法则;反函数、复合函数;对数求导法; 隐函数与参变量函数的导数;微分的概念,微分公式及运算法则,高阶导数。
2、考试要求:
(1)掌握导数、微分、高阶导数概念及导数与微分的几何意义;
(2)熟练掌握导数的四则运算。
(3)掌握反函数、复合函数、隐函数求导法则及对数求导法。
第四章 微分中值定理与导数的应用
1、考试内容:中值定理;洛必达法则;泰勒定理;导数的应用;
2、考试要求:
(1)掌握罗尔定理,拉格朗日中值定理和柯西中值定理。
(2)掌握用洛比达法则求极限。
(3)了解泰勒公式。
(4)熟练掌握用导数研究函数的增减性,曲线的凹凸,极值,拐点,最值问题,渐近线。
第五章 一元函数的积分
一、不定积分部分
1、考试内容:不定积分的概念、性质与计算。
2、考试要求:
(1)掌握原函数和不定积分的概念、性质。
(2)熟练掌握不定积分基本公式,换元积分法和分部积分法。
二、定积分部分
1、考试内容:定积分的概念、性质,变上限积分的导数,牛顿—莱布尼茨公式,定积分的计算,定积分的应用,反常积分。
2、考试要求:
(1)掌握定积分的概念和性质。
(2)熟练掌握变上限积分的导数及牛顿—莱布尼兹公式。
(3)熟练掌握定积分的换元积分法与分部积分法。
(4)了解反常积分的概念及其计算。
(5)握定积分的微元法。
(6)能用定积分求平面图形面积,基本掌握定积分的简单应用。
第六章 空间解析几何与向量代数(本章仅供信息工程学院各专业参考)
1、考试内容:空间直角坐标系、向量的运算、平面方程、直线方程、二次曲面的方程
2、考试要求:
(1)理解空间直角坐标系
(2)掌握向量及其线性运算
(3)掌握空间直线和平面的表示法
(4)理解曲面方程的概念,掌握常用二次曲面的方程及其图形,掌握以坐标轴为旋转轴的旋转曲面及母线平行于坐标轴的柱面方程。
(5)掌握空间曲线的一般表示方法
第七章 多元函数微分学
1、考试内容:多元函数的极限、偏导数、全微分、多元函数与隐函数的微分法
2、考试要求:
(1)理解多元函数的概念,会求多元函数的定义域。
(2)理解偏导数和全微分的概念,会求偏导数和全微分。
(3)掌握复合函数一阶偏导数的求法,会求复合函数的二阶偏导数。
(4)会求隐函数的偏导数。
*(5)理解多元函数极值与条件极值的概念,会求多元函数的极值。了解求条件极值的拉格朗日乘数法,会求解一些较简单的最大值和最小值的应用问题。
第八章 重积分
1、考试内容:二重积分
2、考试要求:
(1)理解二重积分的概念及性质。
(2)了解重积分的换元法,掌握二重积分的计算方法(直角坐标、极坐标)。
(3)会用重积分和曲线积分以及曲面积分求一些几何量与物理量(如体积、曲面面积、重心、转动惯量、引力)。
第九章 微分方程
1、考试内容:一阶线性方程、二阶线性微分方程解的结构、二阶常系数齐次线性微分方程
2、考试要求:
(1)了解微分方程、解、阶、通解、初始条件和特解等概念。
(2)掌握变量可分离的方程及一阶线性方程的解法。会解齐次方程和伯努利(Bernoulli)方程,了解用变量代换求方程的思想。
(3)会解全微分方程。
(4)会用降阶法解高阶微分方程。
(5)理解二阶线性微分方程解的结构。
(6)掌握二阶常系数齐次线性微分方程的解法,并了解高阶常系数齐次线性微分方程的解法。
四、题型、题量与分值
1、试卷题型比例
序号 |
题型 |
分数分配 |
题量 |
1 |
单项选择题 |
20 |
10题 |
2 |
判断题 |
10 |
10题 |
3 |
填空题 |
20 |
10空 |
4 |
计算题 |
36 |
6题 |
5 |
应用题 |
14 |
2题 |
2、章节分值分配
章节 |
内容 |
大概分数分配 |
1 |
函数与极限 |
5 |
2
|
导数 |
15 |
3 |
导数的应用 |
15 |
4 |
不定积分 |
10 |
5 |
定积分及应用 |
30 |
6 |
多元微积分 |
20 |
7 |
微分方程 |
5 |
五、参考教材
①《医药高等数学》陈丽君主编,科学出版社,2021年9月版
②《高等数学》(上、下)(第七版) 同济大学数学系编,等教育出版社
附1 湖北中医药大学《高等数学》试卷样卷
格式要求:宋体小四号,单倍行距,word排版,A4纸型
一、判断题(对的填√,错的填×,每小题1分,共10分)
1.
 在
在
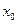 点有定义是极限
点有定义是极限
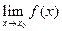 存在的必要条件。( )
存在的必要条件。( )
二、选择题(每小题2分,共16分)
1. 当
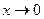 时,下列变量中不是
时,下列变量中不是
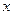 的等价无穷小的是( )
的等价无穷小的是( )
A.
 B.
B.
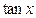 C.
C.
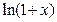 D.
D.
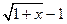
三、填空题(每小题3分,共24分)
1.
 是由 复合而成的;
是由 复合而成的;
四、计算题 (每小题6分,共36分)
1.
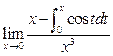 2.
2.
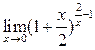
五、应用题(共14分)
设平面图形是由曲线
 ,
,
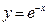 ,
,
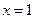 所围成。求:
所围成。求:
(1)(2分) 画出此平面图形;
(2)(4分) 求此平面图形面积;
(3)(8分) 此平面图形绕X轴旋转而成的旋转体的体积
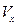 。
。